YES!! , two first order systems in series never yields an underdamped system.

The original transfer function is given below.

Roots of the characteristic polynomial are the exponents in the time-domain solution. These values determine the stability of the output for a bounded input.

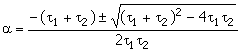
Note that the term inside the square root can be rearranged to be prove that the term is positive as shown below.

Substituting yields the following expression

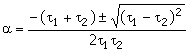
Thus, the roots are a = -1/t ₁ and a = -1/t ₂.

These roots are real and negative; the system is stable and either overdamped (when t1 and t2 are not equal) or critically damped (when t1 and t2 are equal).